• The scaling hypothesis and the laziness of deep learning
• What do neural networks learn?
• NNs learn shortcuts because they are “easy to vary”
• Representing knowledge as probabilistic programs
• Learning as probabilistic program synthesis
• Learning libraries of concepts
• Probabilistic synthesis and causality as program editing
• Implications for AI alignment

Will scaling deep learning produce human-level generality, or do we need a new approach? You may have read the exchange between Scott Alexander and Gary Marcus, and felt that there are some good arguments on both sides, some bad ones, but few arguments that go beyond analogy and handwaving - arguments that would take what we know about deep learning and intelligence, and look at what that knowledge implies. If you haven’t read the exchange, here it is: SA, GM, SA, GM.

I will argue for Marcus’ position, but dive a little deeper than he does. I believe that symbolic representations, specifically programs, and learning as program synthesis, can provide data efficient and flexible generalization, in a way that deep learning can’t, no matter how much we scale it. I’ll show how probabilistic programs can represent causal models of the world, which deep learning can’t do, and why causal models are essential to intelligence. But I’ll start by examining the opposing view, that scaling deep learning is sufficient for general intelligence. To that end, I’ll quote from Gwern’s thorough essay on the scaling hypothesis.

The scaling hypothesis and the laziness of deep learning

The scaling hypothesis is that

we can simply train ever larger NNs and ever more sophisticated behavior will emerge naturally as the easiest way to optimize for all the tasks & data

Gwern cites a swathe of papers in support, interpreting them in such a way that the following picture emerges:

“neural nets are lazy”: sub-models which memorize pieces of the data, or latch onto superficial features, learn quickest and are the easiest to represent internally. If the model & data & compute are not big or varied enough, the optimization, by the end of the cursory training, will have only led to a sub-model which achieves a low loss but missed important pieces of the desired solution.

Eventually, after enough examples and enough updates, there may be a phase transition (Viering & Loog 2021), and the simplest ‘arithmetic’ model which accurately predicts the data just is arithmetic. (…) if there is enough data & compute to push it past the easy convenient sub-models and into the sub-models which express desirable traits like generalizing, factorizing perception into meaningful latent dimensions, meta-learning tasks based on descriptions, learning causal reasoning & logic, and so on

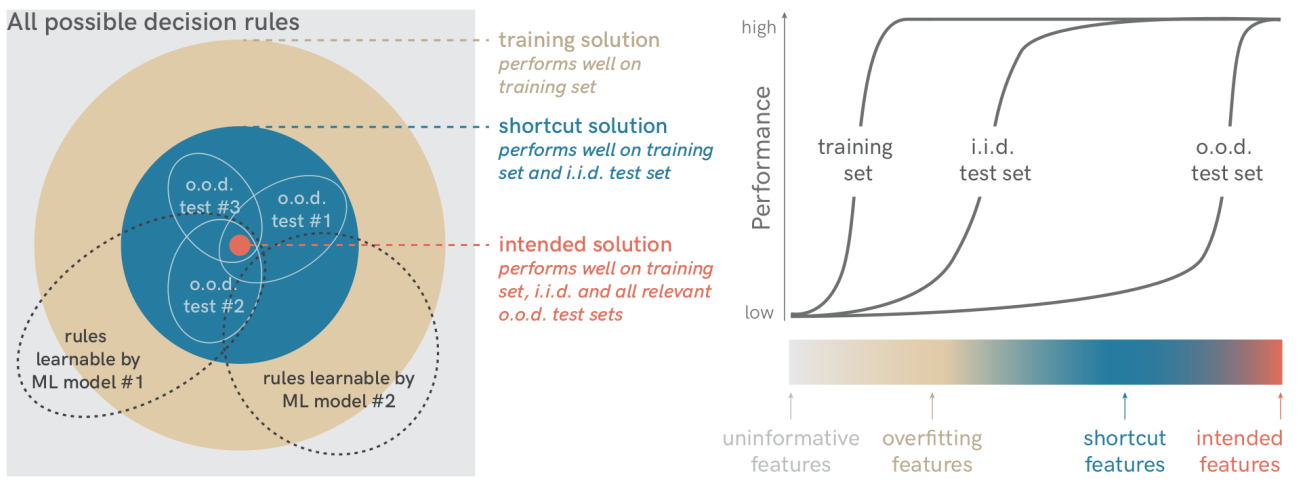
I agree with the premise. Neural nets are indeed “lazy”, in that their loss functions are minimized by “shortcuts”, solutions that don’t generalize beyond the data distribution. A figure from the paper “Shortcut Learning in Deep Neural Networks” by Geirhos et al. illustrates this well:

Credit: Geirhos et al.

Among the set of all possible rules, only some solve the training data. Among the solutions that solve the training data, only some generalize to an i.i.d. test set. Among those solutions, shortcuts fail to generalize to different data (o.o.d. test sets), but the intended solution does generalize.

So, the scaling hypothesis says that at large enough scale, the lazy, shortcut solution is the desired one.

This requires that the desired solution

1. Can be represented by a practically sized NN
2. Has a lower loss than shortcut solutions
3. Can be found by gradient descent

Using the illustration above, we can imagine scaling the model size as the set of rules learnable by ML model #2 expanding, since more parameters means more representable functions. Scaling data and compute corresponds to the set of training and shortcut solutions contracting, since a larger dataset is fit by fewer rules than a small dataset. Visually, the scaling hypothesis requires that (1) the rules learnable by the NN eventually include the orange dot, and that (2 and 3) the blue and beige sets contract around it.

I will argue that this never actually happens. As long as we use NNs, which are large piecewise functions, as representations, 1. won’t hold in general. Roughly speaking, any function can be approximated arbitrarily well as a piecewise function - but given a finite amount of pieces, the “arbitrarily well” part goes out the window. More importantly, as long as the loss we’re minimizing is empirical risk, meaning we optimize training set performance, 2. and 3. won’t hold. An empirical risk minimizer doesn’t care what the NN is doing outside the training sample, so it has zero incentive to find a solution that generalizes everywhere. The optimizer will not allocate pieces outside the training data where it gains nothing from it.

Let’s look at a concrete example. I’ve fit MLPs, and symbolic regression models, to data from \(f(x) = x^2 + \epsilon\), where \(-50 \leq x \leq 100\) is sampled uniformly in the interval, and \(\epsilon\) is Gaussian noise. First, let’s look at how the two methods overfit on 8 training points.

Neither method is regularized properly, and with only 8 points, they both overfit. Here’s how the methods fit 10000 points:

Both methods predict test data, sampled over the same interval, much better now. If we scale up the NN and the training set, we could keep improving the test set performance, evening out the kinks in the piecewise linear function by adding more pieces. But away from the training sample, outside the data distribution, the NN rapidly diverges from the true data generating function. That hasn’t improved, despite overkill amounts of data, parameters and gradient updates (see code here). The symbolic regression actually hasn’t found the correct function either - it fit a second degree polynomial, but with non-zero coefficients for the constant and linear terms, and you’ll see the deviation if you zoom in far enough - but it extrapolates. The model generalizes not just for \(x \in [-50,100]\), but \(x \in \mathbb{R}\).

Fitting \(x^2\) is just a toy example, and on high-dimensional problems, NNs still perform well on i.i.d. test data, while symbolic regression based on genetic algorithms or other meta-heuristics is not scalable in the same way. But the lack of extrapolation, or more generally lack of o.o.d. generalization, is a far worse problem in high-dimensional spaces, where there are far more directions in which to deviate from the training distribution. To generalize in high-dimensional spaces, such as the space of video recordings from self-driving car cameras, we’d need very informative models indeed.

There is a potential way around these limitations, which corresponds to a weaker version of the scaling hypothesis. Proponents of this version acknowledge that NNs don’t extrapolate, and their generalization ability is confined to an “interpolation zone”. But given enough data to cover the relevant parts of the domain, the fact that we’re not generalizing out of distribution won’t be a problem - the shortcut solution will in practice be indistinguishable from the desired solution.

The only relevant assumptions then are

1. There is enough data and compute to solve the problems that general intelligence can solve
2. The data and compute is available within relevant time frames

This weaker version of the scaling hypothesis seems more reasonable, since it doesn’t posit that deep learning starts generalizing better at scale, or finds solutions that it can neither represent nor reach through optimization. But viewed from a different perspective, it is far more radical, because it implies all of intelligence, including improvisation, imagination, creativity etc., is simply the ability to recall a similar circumstance from memory. No o.o.d. generalization needed.

I will argue that mundane problems that we solve everyday put far harsher constraints on data, time and compute, than NNs can accommodate. Such problems can only be solved by strong generalization.

Gwern points out some of these assumptions himself:

Sure, if the model got a low enough loss, it’d have to be intelligent, but how could you prove that would happen in practice? (Training char-RNNs was fun, but they hadn’t exactly revolutionized deep learning.) It might require more text than exists, countless petabytes of data for all of those subtle factors like logical reasoning to represent enough training signal, amidst all the noise and distractors, to train a model. Or maybe your models are too small to do more than absorb the simple surface-level signals, and you would have to scale them 100 orders of magnitude for it to work, because the scaling curves didn’t cooperate. Or maybe your models are fundamentally broken, and stuff like abstraction require an entirely different architecture to work at all, and whatever you do, your current models will saturate at poor performance. Or it’ll train, but it’ll spend all its time trying to improve the surface-level modeling, absorbing more and more literal data and facts without ever ascending to the higher planes of cognition as planned.

but then seems to regard GPT-3 and more recent models as proof by construction that the assumptions hold. I don’t.

The problem is not that GPT-3 or other large models don’t perform well at task X, or that mistakes A, B and C prove that it’s not “really understanding”, or that “mere pattern matching” isn’t intelligence. These objections are valid, but they’re not relevant if merely scaled up versions of essentially the same models start generalizing. For the same reason, we should not be evaluating how well the models perform the tasks they are trained on, but their ability to generalize. It’s lack of generalization that prevents companies from developing viable self-driving cars, or image-based diagnosis that works in practice - despite massive economic incentive, investment and enough GPU-hours to power small countries.

As we scale up deep learning models, they get better performance on a test set of statistically identical examples. As far as many ML engineers are concerned, that’s all there is to generalization. Failure to generalize out of distribution is just a prompt to collect more data and train a larger model. The same limited generalization ability is much more performant when you have a billion more examples to generalize from - whether you use the data directly to train on, or indirectly by using a pre-trained model.

To keep things straight, let’s distinguish between three versions of the scaling hypothesis:

1. Deep learning will never learn to extrapolate, but with enough data, parameters and compute, interpolation is enough.
2. Deep learning will learn to extrapolate, as long as there always are large amounts of data and compute available, which there is.
3. Deep learning will learn to extrapolate, and the more data and compute has been used, the less additional data and compute is needed, i.e. generalization ability increases with scale.

The first versions require less of neural networks themselves, but require the world to be more easily learnable. The latter versions don’t require the world to be easily learnable, but they require neural networks to generalize better at scale. Without any math, let’s look at what NNs do, and see if we can shed some light on these ideas.

What do neural networks learn?

Neural networks are non-linear transformations from one vector space to another. The transformation is performed in steps, layer by layer, from vector space to vector space. Francois Chollet compares the transformation an NN performs to uncrumpling a paper ball. The output vector space, or latent space manifold, is like an uncrumpled, flat piece of paper. On the latent manifold, we can draw a straight line between any two points, and every intermediate point will also lie on the manifold - i.e. they will be plausible data points themselves. This property underlies the magic of deep learning. If the NN is a classifier, the right latent space manifold makes classes linearly separable. In the case of regression, given any input in the convex hull (“somewhere in the middle”) of known points, we can predict the output by interpolation on the latent manifold. Generative models can sample from the latent manifold to produce new samples from the (empirical) data distribution. The defining characteristic of the latent manifold is that distances between observations along the uncrumpled manifold are meaningful in a way that makes the given task easy to solve.

Here’s how this uncrumpling process works for images. In the raw pixel space of images, the distance between images is short if the same pixels have similar colors. But in the subsequent vector spaces learned by a deep NN, the distances will depend on increasingly abstract features. In a layer, the representation from the previous layer is compared to a number of “prototype” features (The comparison is simply a dot product between the representation vector and the prototype - if the vectors align, the dot product is large. Doing that for all the prototypes in the layer is what all those matrix multiplications are for). The next representation is the combined output of these similarity comparisons - the patterns encoded by the previous prototypes have been abstracted away. If two data-points matched the same prototypes to a similar degree, they are similar in that space, and the distance between them is short.

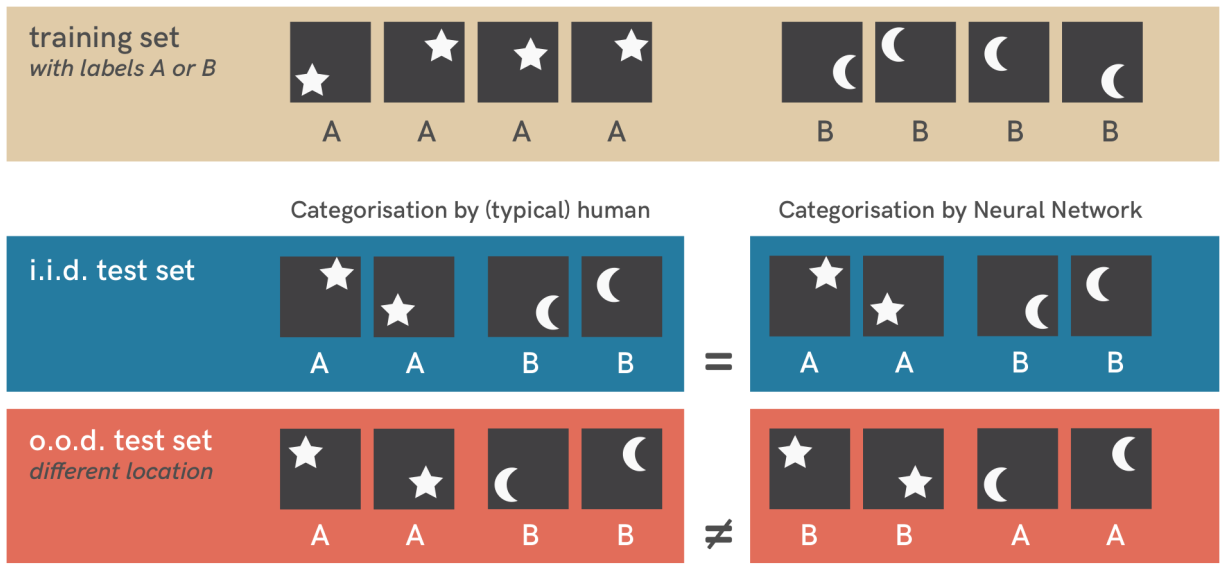
Early layers of convolutional nets learn to detect edges, and later layers detect textures, patterns, parts of objects and objects. It may be that if a test image is similar to a training image in “texture space”, that’s enough to correctly classify it in all training examples. In fact, it has been observed that NNs rely strongly on textures to classify objects, largely ignoring their shape. That’s not a problem, as long as the distribution of test images is the same as the distribution of training images - the textures will always predict the same object that shapes predict. Using textures for classifying objects is not “wrong”, in any way that affects the loss function. It’s a clever shortcut, albeit with limited applicability.

Here’s a toy example of an even simpler shortcut:

Credit: Geirhos et al.

Trained on images of stars and moons (top row), a three-layer MLP correctly classifies new examples from an i.i.d. test set. However, testing it on an o.o.d test set (bottom row) reveals the shortcut: The network has learned to associate object location with a category.

Note that a convolutional net wouldn’t take this shortcut. We explicitly prevent this, by building in translation invariance into CNNs; by iterating over patches of the image, we compute the similarity to the same, reusable “prototype” feature. Thus the NN doesn’t learn a “vertical edge in the upper right corner” feature, and a “vertical edge in the upper middle” and so on. It learns a single “vertical edge” feature, and the for-loops hardcoded into the convolution operation scan the entire image for it. Consider this foreshadowing.

The fact that CNNs learn edge detection filters and other meaningful features has a magical quality to it. Unsupervised learning methods like ICA and sparse coding learn similar features, but they explictly model images as linear combinations of basis images, such that the basis images have minimal mutual information. Seeing the same compression scheme emerge in a deep model, and presumably continue up through all the layers, was and is exciting. It’s easy to take these observations too far, and assume that NNs just always learn the right features. But we know that they don’t. NNs will learn any features that will flatten the latent manifold and minimize the training loss, whether or not they make sense to us, are robust against distribution shift or make the NN vulnerable to adversarial attacks. They won’t learn uninformative features, since those don’t minimize the loss; they won’t learn overfitting features if they’re regularized right and there’s enough data; but they will learn shortcut features. Why? Because they can.

NNs learn shortcuts because they are “easy to vary”

The reason why NNs find shortcuts has to do with the bias-variance tradeoff. The bias-variance tradeoff roughly says that flexible models that express a large hypothesis space, end up learning widely varying hypotheses, when compared across different training sets. Models that are constrained to a small hypothesis space, will learn the same hypotheses, no matter the training set. Thus if you increase the flexibility of an underfitting model by, say, adding parameters, the test error will decrease to a point, and then increase. At first, increasing flexibility allows the model to fit more signal, but at some point the added capacity is used to fit noise.

A better formalization of this is Bayesian Occam’s razor. Rather than varying the complexity of a model, one looks at the probability of generating a given dataset, using each model under consideration. Within each model, if the probability of generating some datasets is high, the probability of generating other datasets must be low. So if one of the models generates a specific dataset with high probability, then assuming no a priori preference for some models over others, it is the most likely model given that dataset. Linear data is best explained by a linear model, sinusoidal data by a sine wave, even though both could be fit equally well by polynomials, or neural networks. It’s not that simple models are better than complex ones, period - it’s that models that are simple in the same way the data is simple are better than models that are complex in ways the data is not. In the extreme, a perfect model contains exactly one hypothesis, the one that produces the exact data we observed (in which case no learning is possible or needed).

A probabilistic perspective of generalization.

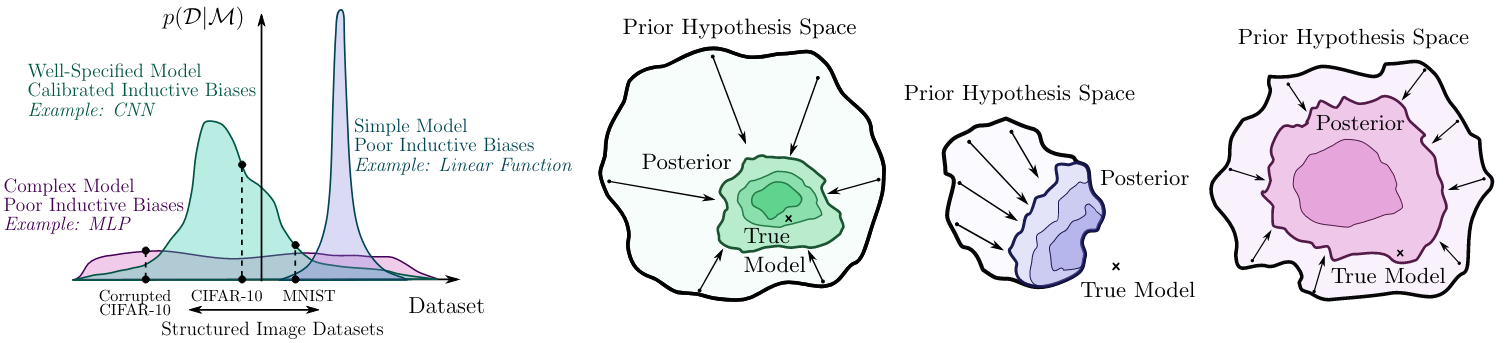
Credit: Andrew Gordon Wilson and Pavel Izmailov

Neural networks sit closer to the other extreme. You can get a neural network to produce pretty much any data, which is why they are so widely applicable. Of course, there has to be more to deep learning than just flexibility, otherwise any sufficiently flexible learning algorithm would perform as well as deep learning does. The answer is that despite being very flexible, neural networks are still biased towards learning certain structures over others. The most important of these inductive biases is towards hierarchical structure, as explained in the previous section - different complex objects are made of similar simple objects. Another is the smoothness bias - if you change the input just a little, the output also doesn’t change much. As mentioned, CNNs are endowed with a powerful bias towards natural images, in which the hierarchical structure bias further disregards the position in the image (and importantly, the image is processed as a 2D matrix rather than a vector). This bias is so apt that even without training CNNs on any data, they perform very well on several computer vision tasks. Transformers are equipped with a bias towards simple sequence to sequence functions - at each level of the hierarchy, the input is treated as a query sequence, to be compared against stored key sequences, returning a corresponding value sequence. This results in a kind of associative memory, as known from Hopfield networks.

Inductive biases not only make learning more efficient, they are what allows the model to generalize. Some believe that deep learning is somehow exempt from this, in that highly over-parametrized networks tend to work better, not worse, most clearly shown in the double descent phenomenon. A naive understanding of the bias-variance tradeoff predicts that highly flexible models should perform worse. But double descent is not at all unique to deep learning, and it doesn’t contradict the bias-variance tradeoff or Bayesian model comparison framework in any way. What causes the apparent contradiction is not accounting for regularization, ensembling, and marginalizing over the posterior, all of which reduce variance. Whether it’s deep learning, or any model without fixed capacity, a point estimate of the model parameters at the level of complexity that is just enough to fit signal and noise, will overfit. Beyond that complexity threshold, models enter an “interpolation zone”, where the test performance keeps improving, if the model is regularized properly. If instead of fitting a point estimate, one considers the full posterior, or approximates it as an ensemble of point estimates, the mystery of double descent falls away - the performance of the ensemble improves monotonically with added complexity.

The fact that the point estimate has high variance is especially true in deep learning, where the estimate is highly underdetermined by the data (the same dataset can be fit by many, many different parameter settings). From a Bayesian perspective, the model evidence for large, flexible neural networks, is much lower than for simpler models - if your model can fit everything, it’s not a good explanation for anything.

Neural networks being able to predict anything while explaining nothing, turns from a philosophical to a practical problem once we consider generalization beyond an i.i.d. test set. It is then that it becomes obvious that the neural network has learned a shortcut - it has gamed the empirical risk minimization task, without breaking any rules, but by breaking the spirit of it, which of course only exists in the programmer’s mind (if at all).

Having said all this, couldn’t it still be the case that, with enough training examples, a shortcut solution just is the desired solution, with out-of-distribution generalization, extrapolation through causality, even symbol manipulation? After all, with every additional training example, we are eliminating possible bad shortcuts.

The answer is no. As John von Neumann allegedly said, “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk”. Each extra parameter adds far more possible shortcuts than an extra training example eliminates. Could we do the opposite then? Add more training data, but keep the network as small as possible? Also no. The network simply becomes too limited in representational capacity to learn much signal. The parameters quickly converge, and the remaining data is virtually unused. The bias-variance tradeoff lives up to its name - we can either have a small network that underfits, or a large network that learns a shortcut. One can keep playing the scaling game, fitting more and more examples with more and more parameters, but the real world is not so obliging as to present i.i.d. examples, with the occasional o.o.d. outlier thrown in to keep things spicy. It is exactly the fact that real world presents us with constant novelty that makes intelligence useful, and shortcut learning useless.

The physicist David Deutsch proposes a single criterion to judge the quality of explanations. He says good explanations are those that are hard to vary, while still accounting for observations. This is why the Greek myth that explains the seasons, in which Persephone has to return to the underworld each winter, causing her mother Demeter to turn the world cold out of sadness, is a bad explanation. The problem is not that it isn’t falsifiable. As Deutsch points out, the ancient Greeks could in principle have traveled to the southern hemisphere and observed that it is warmest there when Demeter supposedly is at her saddest. The problem is that most of the details of the explanation could be changed in myriad ways, without any consequences. Perhaps it’s a different Goddess, not Demeter. Perhaps Persephone returns to the underworld in the summer, and the heat from the underworld causes the warm temperatures. And so on.

Contrast this with the modern explanation for the seasons, which is that the tilt of the Earth causes the same amount of sunlight to be dispersed over a differently sized area, depending on whether the tilt is towards the sun, or away from it, as the Earth orbits the Sun. Every part of the explanation plays a functional role. It’s hard to vary any part, without affecting the logic. It also happens to explain more than just the seasons; it explains the motion of the sun across the sky throughout the year, the change in climate caused by the variations in the tilt of the earth and more.

Neural networks are very easy to vary, which is why they never constitute good explanations - and why they always are shortcuts instead. In order to have agents that can create generalizable knowledge, we first need a way to represent knowledge, such that it’s hard to vary.

Representing knowledge as probabilistic programs

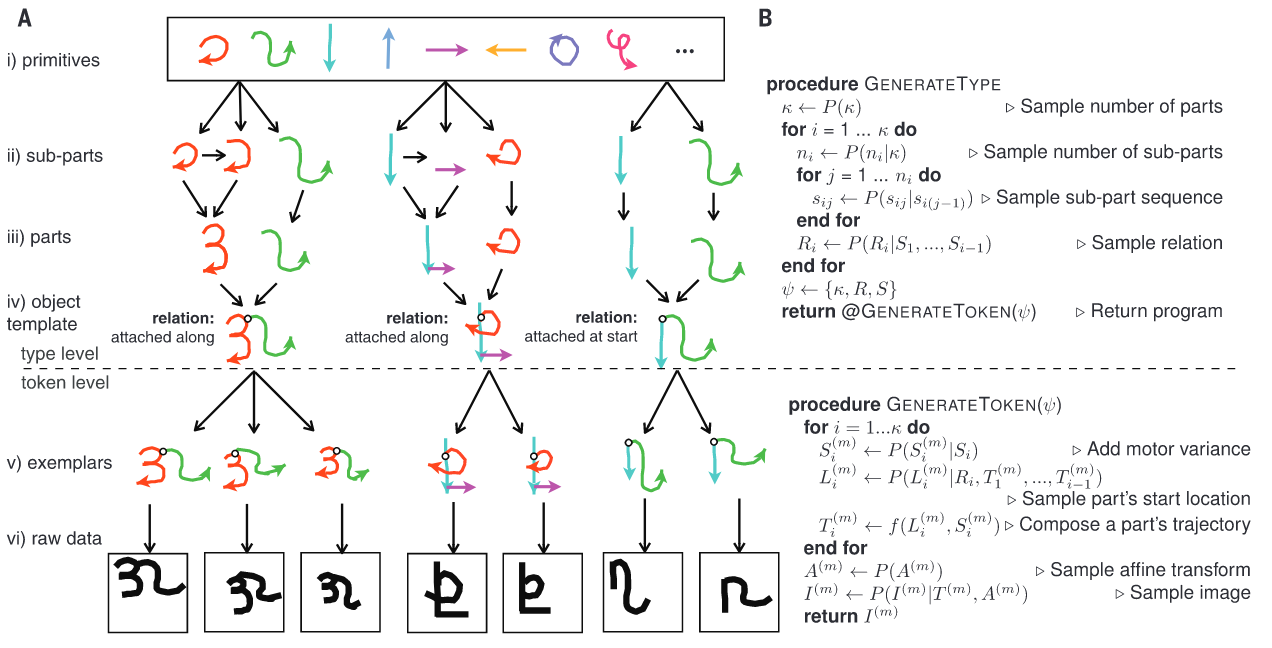
A 2012 paper called “Human-level concept learning through probabilistic program induction”, presents a model of handwritten characters that learned to generate new samples after having seen as little as one example, of a quality indistinguishable from human ones. The success of the model can be attributed to the fact that it encodes the actual handwriting process, down to each individual stroke of the pen.

Credit: Lake et al.

Constructing the model thus required an expert to first understand how the writing process works, figure out what the basic moves are, how they can vary, how they combine, and how to render the character as an image. The expert then needs to be knowledgeable in both programming and statistics to formulate both the probabilistic program, which represents the writing process in code and the various sources of variation and noise as random variables, and then the inference algorithm, the program which inverts the writing process, from a given image to the strokes and randomness that produced it - which usually is the hardest part.

Following Chollet’s definition of intelligence, this program is just as unintelligent as a deep learning model. While we bought sample efficiency, robustness to distribution shift, and extrapolation ability, we payed for it with an almost complete lack of generality, a large amount of required domain expertise, and an even larger cost in technical expertise. The model can well be said to “understand” handwriting, as opposed to a deep learning model, but it’s clear that all the understanding comes directly from the developer. It is the developer’s brain that created the causal knowledge of handwriting and represented it as a probabilistic program. Worse still, it is also the developer that figured out how to solve the complex problem of searching the large combinatorial space of different numbers and types of parts, sub-parts, and relations, to efficiently find the particular combinations that are likely to have produced a given image, and represented this solution as a highly specialized inference algorithm. This is narrow AI at its narrowest.

But notice how easy it would be to extend and combine the knowledge represented in this program, with other knowledge and skills. Generating a sequence of handwritten characters would just be calling the procedure several times, and concatenating the images. Inferring the motions that generated a sequence could also straightforwardly reuse the single character inference algorithm as a subroutine. Compositionality and modularity are also big selling points for explainability. To understand the whole program, just understand the parts and how they combine.

The narrowness of the program is also what makes it phenomenally robust to noise and distribution shifts. Changes to the font color, or line thickness, or background, which would undoubtedly break a deep learning model, would have no effect here. Invariance to rotation, scale, skewness, are all built-in to the model, no data augmentation needed. Adversarial attacks are not a thing. The knowledge contained in the program also generalizes far beyond the data distribution - a similar, neuro-symbolic model trained on MNIST exhibits zero-shot transfer to other tasks - including a doodle-drawing task, as well as the one this model is trained on. Without being retrained on any of the other datasets, it’s able to generate new samples from all these other data distributions, out of the box. While the model and the inference algorithm are highly specialized, very narrow AI, the explanation they embody is so good that it generalizes far outside the original task - and as mentioned above, easily extendable much farther.

That’s the power of symbolic representations. By writing computations as code, they become data that can be manipulated and analyzed by other code. Programming languages become programs which take code as input and return code as output. It seems that our cognition exhibits the same property, most obviously language, but clearly perception, motor skills and planning as well. Cognitive skills are programs - programs that generate mental imagery, verbal thought, behaviors and plans, as well as programs that infer the world from visual, auditory and other sensory input, infer mental states and goals in other agents, and in ourselves.

The generative and inference programs from the above example were written by skilled humans. But where do cognitive skill programs in humans come from? How do you learn programs?

Learning as probabilistic program synthesis

If skills are programs, and intelligence is the ability to efficiently learn skills, then intelligence is, broadly speaking, programming ability. Deep learning can be seen as a special case, in which the programs are restricted to differentiable, composite functions, and the space of programs is searched by SGD, an optimization algorithm that exploits the differentiability of the loss function wrt. parameters, and backpropagation that exploits the compositionality of NNs for efficient gradient computation. Learning the parameters without the use of gradients, say by random search, or worse, grid search, would be completely infeasible.

In probabilistic programming, where the probabilistic program, priors and observed data are provided, learning is some approximation to full Bayesian inference. Learning the full posterior by conditioning on observed data involves integrating over a potentially high-dimensional continuous space, and/or summing over a high-dimensional discrete space, which usually isn’t feasible. Popular ways to approximate the Bayesian posterior are MCMC, in which a stochastic process generates samples from the posterior distribution, and variational inference, in which we optimize an approximating distribution to diverge as little from the posterior as possible. Approximate Bayesian inference is a lot more involved than SGD. Most probabilistic programming languages come with just one or a couple of efficiently implemented inference algorithms, with limited generality, but some experimental ones allow you to program your own custom inference algorithms, even ones that involve neural networks to great effect. Skilled probrammers can decompose inference into subproblems, tackle each one with different algorithms or alternate between updating on old data and incorporating new data in smart ways, collectively called inference programming. Such techniques can start to blur the line between learning as parameter estimation and learning as programming, when applied to models with stochastic structure - models in which random choices determine the make-up of the rest of the model, such as in the handwritten character program above, in which the number of parts is itself a parameter (rather than having separate models for “two-stroke-characters”, “three-stroke-characters” and so on).

When it crosses over to learning as programming proper, it’s called program synthesis. The primary challenge in program synthesis is to search the gargantuan, combinatorial space of programs. Doing this by brute force, would be a bit like trying to train a neural network by grid search. If we have a programming language of \(b\) keywords, and think of a program as a concatenation of keywords, then finding a program of length \(d\) by just trying every possible program, would take on the order of \(\mathcal{O}(b^d)\). That’s CS speak for “ain’t gonna happen”.

That’s bad news for the learning efficiency of the program synthesis approach. If the programming language is specialized to the given task, and has a simple syntax, the program will be short. But when learning a domain from scratch, we’d like the language to be Turing-complete. In deep learning, and machine learning in general, the ability of a model to express only certain kinds of functions allows specialized algorithms to efficiently search for the function(s) that match a given training set. In program synthesis, much like hypothesis formulation in science, there are no limits on what kinds of programs we could synthesize, but on the other hand, we have a large amount of control over what kinds of programs will be considered. Success in program synthesis (much like success in science), is highly dependent on the ability to deploy that control effectively, to avoid searching most of program space, and instead focus on the very best candidates.

Learning libraries of concepts

We’ve identified two tradeoffs that exist in traditional machine learning, but go up a meta-level in program synthesis. Much like the bias-variance tradeoff for models, in program synthesis we can choose between specialized, domain specific languages (DSLs), in which programs that solve tasks in a narrow domain are simple and concise; or universal, Turing-complete languages, in which we can write programs that solve any task humans can solve, if only their length wouldn’t make discovering them intractable. And much like the tradeoff between compute-hungry but broadly-applicable learning algorithms like SGD versus efficient but bespoke inference programs that exploit the structure of a given learning problem, in program synthesis there’s a generality-efficiency tradeoff in the choice of search algorithm. We can choose between general-purpose methods like brute-force enumeration that construct and evaluate entire programs, one by one, or more specialized methods which efficiently represent and evaluate entire subspaces of program space at a time.

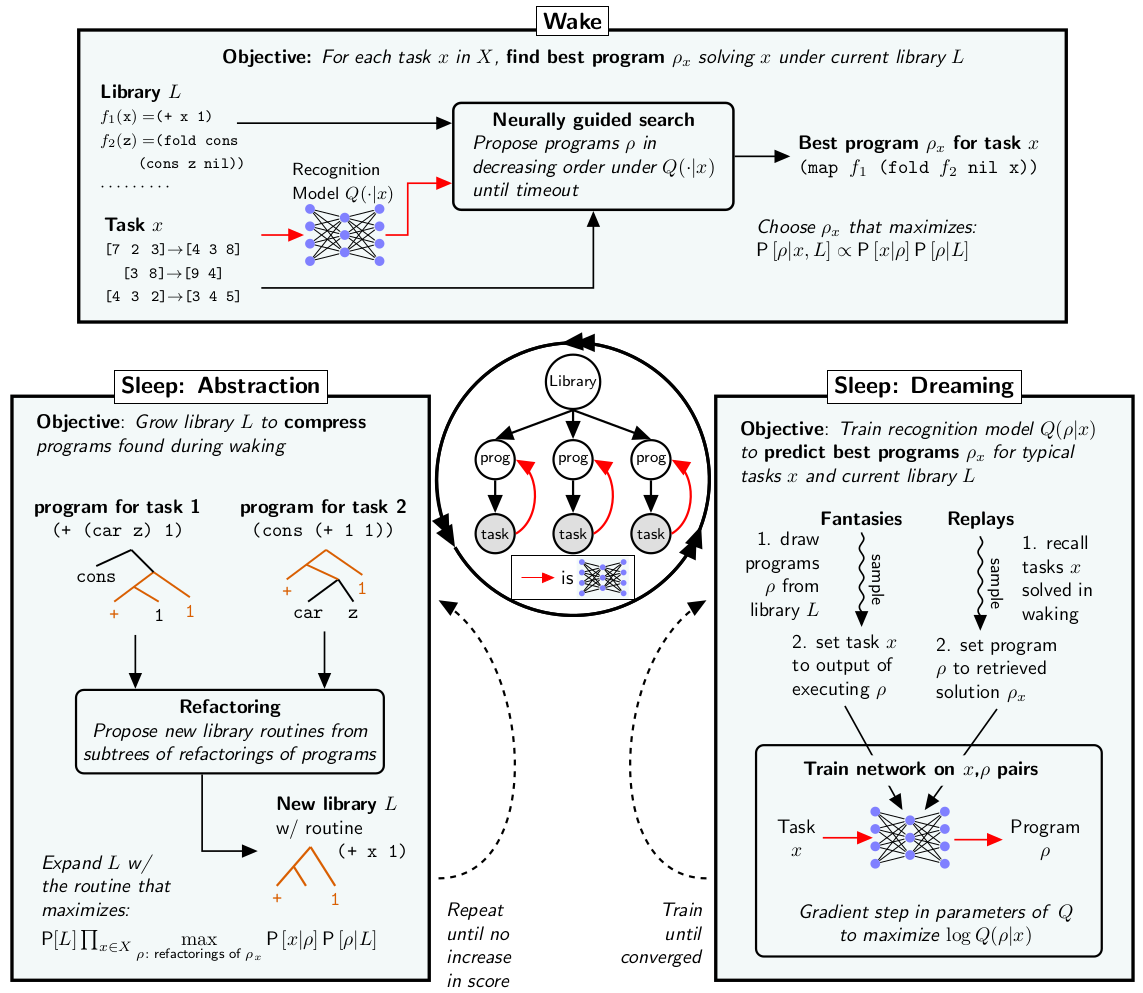
Most successful applications of program synthesis, like the FlashFill feature in Excel, rely on human experts to design a custom DSL, as well as a custom search algorithm. A paper from Ellis et al. proposes an alternative - learn a DSL, and learn how to write programs in it. Called DreamCoder, the algorithm alternates between three phases:

• Wake, in which new tasks are solved by searching for programs expressed in the current version of the learned DSL, helped by the current version of a neural network which guides the search
• Abstraction sleep, in which the learned DSL is expanded by looking at code snippets that were useful in solving the tasks during waking, and abstracting them into new functions in the DSL, and
• Dream sleep, in which we generate programs and data using those programs, and train the neural network to help find the programs given the data.

Credit: Ellis et al.

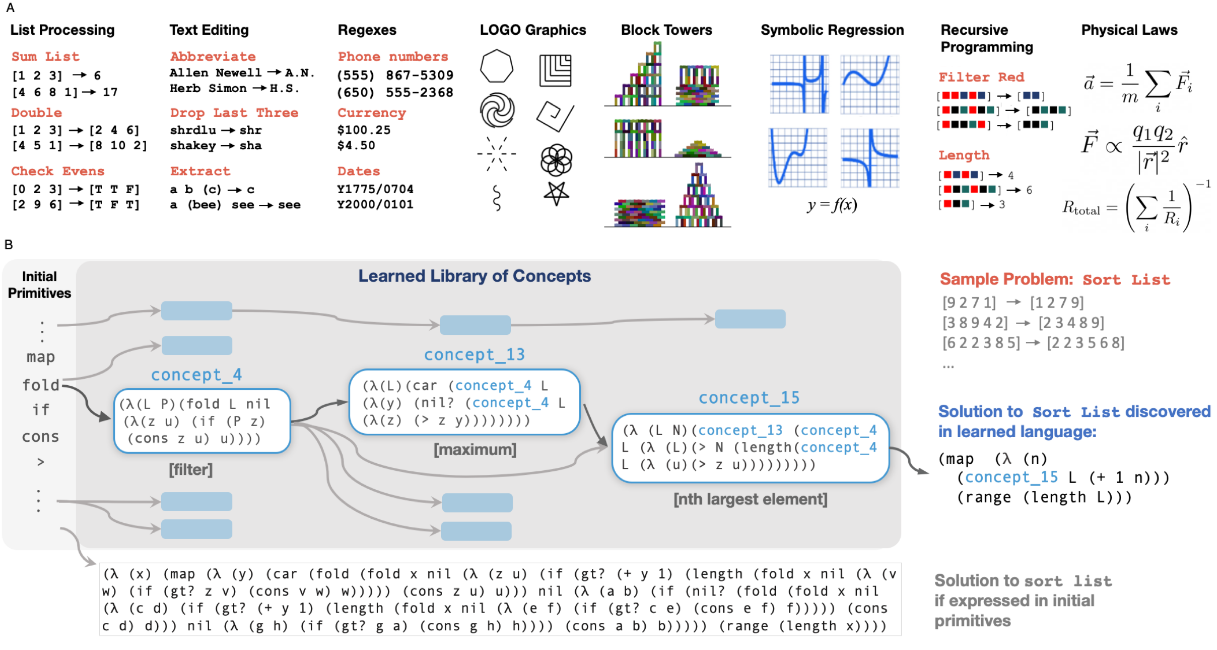
With this design, DreamCoder can learn to acquire skills in a wide variety of domains, with or without supervision. It can learn to process lists, edit text, find regexes, draw simple graphics, build structures out of blocks, do symbolic regression, discover physical laws and much more.

Credit: Ellis et al.

The programs it discovers generalize. For example, the sorting algorithm it discovers can sort any list, not just ones that are statistically identical to the few examples it sees. Much of this generalization ability stems from the way the three phases bootstrap each other - with each iteration, previously unsolvable tasks get solved thanks to better inductive biases in the DSL and better guidance from the neural network; the DSL becomes more finely tuned to the domain, thanks to new programs being discovered during waking which get refactored into transferable concepts; and the neural network gets better programs to train on thanks to both a wider range of solved tasks and more realistic “dream” tasks sampled from the DSL. Because the NN is supplied with ad libitum training data from an ever-expanding corpus, and the output space of concepts is growing with each iteration, it’s not just learning a static distribution like LLMs do. Similar to the interplay of MCTS and the value network in AlphaGo, this prevents it from merely interpolating in a fixed subspace of program space.

Using DreamCoder for new domains still requires a little human expertise. One needs to provide the initial concepts that form the primitives of the DSL, which can be very general - to discover physical laws, it was sufficient to provide it with a few higher-order functions like map and fold, and basic arithmetic, and DreamCoder itself learned concepts from vector algebra, like inner products and norms, and physics, like inverse-square laws. The neural network part relies on some deep learning expertise, knowing how to embed tasks and select an appropriate architecture for the domain. More subtly, it’s also up to the expert to delineate what tasks belong to which domains. The authors speculate how this limitation could be overcome in future work:

the approach will need to be extended to learn not just one domain at a time, but to simultaneously develop expertise across many different classes of problems, autonomously carving out its own domains alongside its own domain-specific representations. We anticipate this will be enabled by metalearning a cross-domain library or “language-of-thought” (…): growing a single generic programmatic substrate for learning and reasoning, as humans have built collectively through biological and cultural evolution, which can then differentiate itself into representations for unboundedly many different classes of problems.

Perhaps the most exciting aspect of DreamCoder is that, despite the many and diverse sources of inspiration, how much work has gone into it, and how impressive the result is, it opens up so many new avenues for research. If anything marks an approach as anticipating a future paradigm shift, that would be it.

Probabilistic synthesis and causality as program editing

The wake phase of DreamCoder, which synthesizes programs using neurally guided beam search (more or less, the exact algorithm is a little more elaborate), is an example of deterministic synthesis. Given the same task, DSL and recognition network, the resulting program is the same every time the search is run. For some domains, the synthesized program is the final output - this can be a deterministic program, or a probabilistic one. For other domains, like symbolic regression, the synthesized program is itself a model which an inner optimization algorithm fits to data. There is a clear separation between the meta-learning task of learning a symbolic regression DSL and recognition network, performed by the abstraction and dream sleep phases, the structure learning task of synthesizing the functional form of the regression, performed by the wake phase, and the parameter learning task of fitting the parameters to data, performed by gradient descent.

But as mentioned, there isn’t necessarily a clear distinction between these levels, and there may be much benefit to having them closely coupled. If we’re Bayesians (and what civilized person isn’t) we may be interested in synthesizing not just a single program that solves a given task, or generates a given dataset with high probability, but a posterior distribution over programs, given some prior specified by a DSL. Such a distribution allows us to answer queries about the qualitative structure of programs, such as “What is the probability that the data contains clusters?” or “What is the probability that the time series dynamics changed at any point?”.

A 2019 paper, Bayesian Synthesis of Probabilistic Programs for Automatic Data Modeling, shows how this works in theory, and demonstrates the power of the approach in practice. While not as general as DreamCoder, it is far more general than regular probabilistic programming, which relies on modelling and inference expertise pertaining to a single problem. Here, the expert instead designs a DSL that can express probabilistic programs for an entire domain of problems, as well as transition operators, which mutate a candidate program into the next. The authors design DSLs for modeling time-series problems and tabular data, and show how the learned programs are more accurate and extrapolate better than commonly used statistical techniques on quite complex datasets - all while being explainable.

Automating statistical modelling is cool enough, but the holy grail is to learn programs that act in the real world. What do those sorts of programs look like? They might look a bit like video games - or more precisely game engines. Two of the most important components in game engines are a graphics engine, which renders visual scenes given a 3D model, and a physics engine, which approximates the physics of objects in the scenes, in real time. In perception, as in video games, we need quick, actionable information, so we don’t care so much about scientific accuracy or precision, as much as speed and robustness. We want probabilistic graphics engines, and probabilistic physics engines, which don’t work by solving differential equations given precise initial conditions, but by representing the uncertainty in the current state and dynamics, and simulating likely near-term futures.

More importantly, we want inverse graphics and physics engines, which given a 2D visual scene returns a 3D model of the world, and given trajectories of objects returns the forces acting on them. These are ill-posed problems, since we’re trying to infer high-dimensional latent variables from lower-dimensional observed ones. There isn’t enough information in the data to infer what caused them. It’s only by having good models of the forward, causal processes, i.e. optics and mechanics, as well as handling uncertainty in the observations so that they can be matched against the predictions of the causal models, that we can begin to solve these problems. The payoff is worth it though - imagine the wealth that would be created by sample-efficient and robust learning of sensorimotor skills. Self-driving cars would just be the start.

We’d like to be able to synthesize graphics and physics engines, as well as their inverse counterparts, and in general, we’d like to be able to learn complex causal models. The ability to synthesize large causal models is probably still a ways away, but another paper from MIT’s Probabilistic Computing group points the way. Like the previous paper mentioned above, the framework is Bayesian synthesis of probabilistic programs, but the inference accounts not just for observations, but also interventions. You may have heard of Judea Pearl’s do-calculus, in which the do-operator represents intervening on a causal system. In an experiment, whether one performed by a toddler or by researchers running randomized controlled trials, controlling a variable changes the probability distribution of the data. The do-operator is an elementary intervention, in which the variable is set to a given value - e.g. the treatment variable is set to 1 for the treatment group, and 0 for the control group. But more generally we can intervene on variables in all the ways we can change probability distributions - shift the mean, scale the variance - and all the ways we can edit programs - walk through the code, substitute some expressions for others in specified ways, add new variables, remove previous ones, etc.

We can then express these interventions as program-editing programs, which allows us to incorporate data from physical and simulated experiments, in the Bayesian synthesis process. The authors demonstrate how incorporating experimental data helps identify the correct causal model (or rather, concentrates posterior probability mass over the correct causal models), in a toy example.

The scientific revolution took off when people stopped being satisfied with the “more epicycles” approach to modelling, and started doing experiments. If history is to repeat itself in silico, we should be prepared for it.

Implications for AI alignment

The intended audience of this post doesn’t need convincing that AI alignment is important. From what I’ve seen, there’s considerable overlap between those who take AI alignment seriously, and those who think scaling deep learning will produce AGI. My own view on AI alignment is that it’s probably only possible to do it in close concert with capabilities research. From this point of view, all of the above issues with the capabilities of deep learning is good news, because most of them are also alignment issues. I’ve strived to make a case that there is a clear path, or the beginning of a path, towards solving them. If we want AI systems to understand us, and understand what we want, they will need to learn causal models of us, and why we want some things and not other things. They will need to be robust to distribution shift, and think in terms of hypotheticals and counterfactuals. I’m hoping, but obviously don’t really know, that there will be powerful economic incentives to align AI systems in this way, and that capabilities research and alignment research will keep pointing in similar directions for a while still. Right now, we have a golden opportunity to get started on this before everyone else does.

Thanks to EducationalCicada for suggestions and feedback!